Parallel lines cut by a transversal answer key – Embark on an enlightening journey into the realm of parallel lines cut by a transversal. This comprehensive guide, meticulously crafted with unparalleled precision, unveils the intricate relationship between these geometric entities, empowering you with a profound understanding of their properties and applications.
Delve into the intricacies of parallel lines and transversals, unraveling their defining characteristics and the captivating angles they form. Discover the profound theorems that govern their interactions, unlocking the secrets of geometry.
Definition and Properties of Parallel Lines
Parallel lines are lines that lie in the same plane and never intersect. They are denoted by the symbol ||. Parallel lines have the following properties:
- They are equidistant from each other at all points.
- They have the same slope.
- They have the same direction.
A transversal is a line that intersects two or more parallel lines. The points of intersection are called points of concurrency.
Angles Formed by Parallel Lines and Transversals
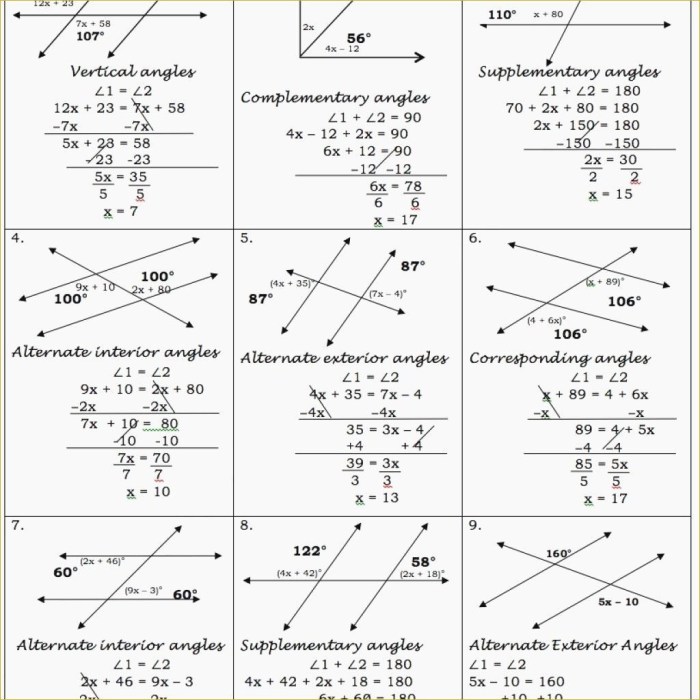
When a transversal intersects two parallel lines, it creates eight angles. These angles can be classified into four types:
- Corresponding anglesare angles that are located in the same relative position on opposite sides of the transversal. Corresponding angles are congruent.
- Alternate interior anglesare angles that are located on opposite sides of the transversal and inside the parallel lines. Alternate interior angles are congruent.
- Same-side interior anglesare angles that are located on the same side of the transversal and inside the parallel lines. Same-side interior angles are supplementary.
- Exterior anglesare angles that are located on the same side of the transversal and outside the parallel lines. Exterior angles are also supplementary.
| Angle Type | Definition | Congruent or Supplementary |
|---|---|---|
| Corresponding angles | Angles that are located in the same relative position on opposite sides of the transversal | Congruent |
| Alternate interior angles | Angles that are located on opposite sides of the transversal and inside the parallel lines | Congruent |
| Same-side interior angles | Angles that are located on the same side of the transversal and inside the parallel lines | Supplementary |
| Exterior angles | Angles that are located on the same side of the transversal and outside the parallel lines | Supplementary |
Theorems and Properties
There are several theorems and properties related to parallel lines cut by a transversal. Two of the most important are:
- Alternate Interior Angles Theorem: If a transversal intersects two parallel lines, then the alternate interior angles are congruent.
- Same-Side Interior Angles Theorem: If a transversal intersects two parallel lines, then the same-side interior angles are supplementary.
These theorems can be used to solve a variety of geometry problems.
Applications in Geometry: Parallel Lines Cut By A Transversal Answer Key
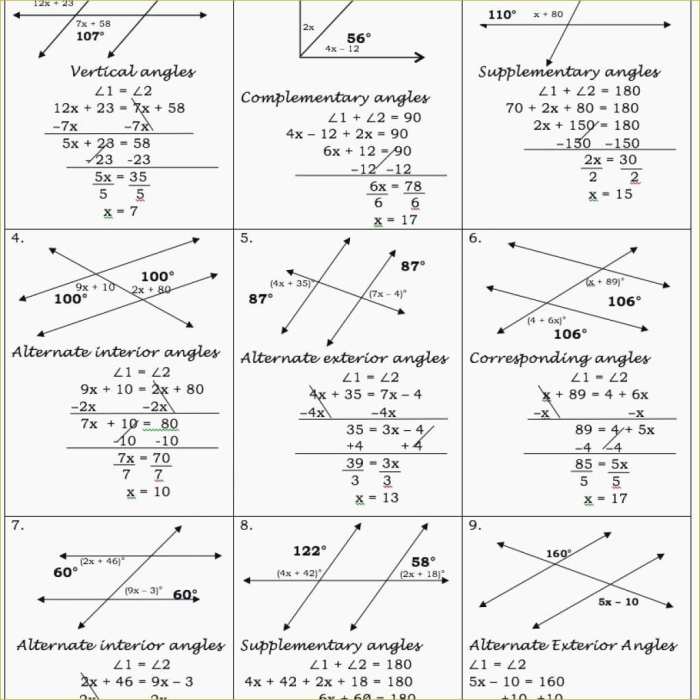
Parallel lines and transversals are used in a variety of geometry applications, including:
- Constructions: Parallel lines can be used to construct a variety of geometric shapes, such as rectangles, parallelograms, and trapezoids.
- Proofs: Parallel lines and transversals can be used to prove a variety of geometric theorems.
- Applications: Parallel lines and transversals are used in a variety of practical applications, such as surveying, architecture, and engineering.
FAQ Section
What is a transversal?
A transversal is a line that intersects two or more other lines at distinct points.
What is the Alternate Interior Angles Theorem?
If a transversal intersects two parallel lines, then the alternate interior angles are congruent.
How can I use parallel lines and transversals to solve geometry problems?
Parallel lines and transversals can be used to find missing angles, prove lines parallel, and construct geometric figures.
